Kakuro Tutorial
I've put this tutorial here because there just doesn't seem to be a decent tutorial on solving Kakuro puzzles on the Internet that I've seen and many people who I have spoken to about Kakuro puzzles don't know where to start so, this is for the complete beginner - including people who have never done a Sudoku puzzle
The rules are simple:
- Only the numbers 1 to 9 may be used in any cell;
- In any given sum (a set of cells running across or down - broadly equivalent to a 'word' in a crossword puzzle), any given number must appear no more than once; and,
- Each sum must add up to exactly the total in the clue.
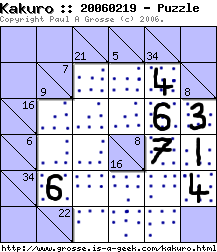
So, we know the rules - how do we solve one? I've started off with a simple looking puzzle (based on the assumption that if it is small, it must be simple - which is a bit naive). There is more to this puzzle than initially meets the eye though and this puzzle will teach a lot.
Apart from its size, this is a typical Kakuro puzzle as generated by the Perl computer program that I run on this site. If you click on it, it will appear on its own in a new browser window so that you can print it out to follow this tutorial by doing it yourself rather than just folowing it. Kakuro puzzles are many ways similar to a normal crossword puzzle except that as the clues are each only a one or two digit number, they are written next to where the sums go.
This close-up shows you just how each clue relates to each sum in the puzzle. We now know how the clues relate to the cells but how do we find out the numbers that go in each cell?
From the rules at the top of this page, we know that each number must be different and that no number can be repeated. If we take the example of 7, it turns out that the only combination of three digits that fullfills the Kakuro rules is: 1, 2 and 4. Although, we still don't know the order.
Are we supposed to be able to remember all of these combinations? There must be hundreds of them.
If you look at the Kakuro Puzzle Number List - All Sets, you will see a table with the number of cells in a given sum, followed by its total, then the list of number sets that can occur in such a set of cells, followed by the excluded numbers. For a unique set like 7 in 3 cells, the excluded numbers are pretty obvious but if you look at, say, 2 cells totalling 12, the excluded numbers are 1, 2 and 6. So, why are the excluded numbers so important?
The answer to that is that any of the cells can be any of the numbers 1 to 9. With a sum, that can be filtered down to a subset (of excluded numbers 1, 2 and 6 for our 12 in 2 example). So, if we managed to filter it down even more - say one of these cells was crossed by a sum of 6 in 3 cells, that would also eliminate the numbers 4, 5, 6, 7, 8 and 9. That means that the only number that can be in that cell is a 3.
So, what is a good way of noting down which numbers are eliminated?
Working on the principle that you can only add ink to paper, it is one idea that you can place a dot (preferably using a light-coloured ink) in the cell to represent each number that has been eliminated - if you only have one place left without a dot, it must be that number. When you get experienced at these, you won't need to use the spots any longer, they are just an aid to get you started.
If you arrange the dots like this - you can get used to this type of notation very easily and it is a lot better than writing little numbers down and then forgetting what they are because they are so small and you crossed them out unclearly and so on - then you can see at a glance where any numbers that have not been eliminated are.
So, Let's start marking it out...
This is how you would mark out the seven in three cells. From the sheet, we know that the eliminated numbers are 356789 so put that pattern in all of the cells for that clue.
Next, we can put in the spots for the five in two cells clue. This one eliminates 56789 so we put in those spots for that sum.
Although this particular elimination hasn't narrowed down the set of numbers for the cell where these two numbers cross, you can see how the spot patterns superimpose.
So, STEP 1 is to insert all of these elimination patterns for each clue.
When you have finished, it looks like this. If you look at it closely, you can see that the last cell of the top row has only a 4 left in it unmarked and that the bottom cell of the 8 in 3 down on the right has only a 4 left in it. Now, we need to write in those numbers and mark up those new eliminations in the sums that that cell intersects.
You can see that the new marks (in red) have eliminated a few more options in some cells and at the bottom cell of the 9 in 3 on the left, we now have only one choice - a 6. Also, under the 4 on the top right, we have another 6.
So, STEP 2 is to eliminate numbers in rows and columns as new numbers appear and to keep on repeating step 2 until this can't happen any more. Thus...
And this is as far as we get.
Now though, we have a situation where we know that a sum (8 in 2 cells on the right) has a 7 in it so the other cell must be a 1. (I said on the home page that this was maths that a six-year-old could do). So, we write in the 1 like so.
Before we go any further, there is something else we need to look at and there are several ways of doing this:
1 We know from the table that that the sum of 8 in 3 cells comprises of either 125 or 134. We already know that we have a 4 in this sum so the only combination that could fit is 134. This means that now we know where the 1 and 4 go, we know that the number at the top is a 3; or,
2 We know that the sum is 8 and that we have accounted for 4 of this already. This leaves 4 in 2 cells which eliminates 2456789. When we put the 1 in the middle cell, we knew that only 3 was left for the top cell.
So, let's put in the 3, mark off any spots in relevent cells and see what happens...
Not a lot. And, we have run out of ways of doing this. So, what else can we infer from the rules?
If you look at the 5 in 2 cells at the top, you can see that there are only two options for the top cell - 1 and 2. We know that the sum is 5 so if we look at our table, we see that the combinations are 14, 23, 32 and 41. If we look at the spots: the 1 in the top matches up with a 4 in the bottom; but the 2 in the top is eliminated by the spot at the 3 position in the bottom cell. STEP 3. Therefore we can infer that the top cell can have the 2 position spotted as this combination cannot occur.
So, let's fill that in and carry on...
The combination for 7 in 3 is 124 so we know that the remaining cell in the row at the top is a 2 so we write that in and spot the column.
Like so.
If we look at the 5 in 2 on the top, we know the 1 so we can mark off the 4 and spot the relevant cells.
Next, the 1 in the cell next to it, and the 2 in the cell next to that. Then, working down, we know that 2 + 6 = 8 so in the middle cell of the 9 in 3, there is a 1 which, in turn, makes the cell to its right, (the 6 in 2) a 5.
Now, it looks like this.
What can we do next?
If we look at the 21 in 5 running down, it already has 1, 2 and 5 in it so we can either look at the combinations of 21 in 5 that have a 1, 2 and 5 in them (12459 and 12567); or, we can take off the 8 from 21 and see what combinations there are in 13 in 3 (49 58 67). We already have a 5 in the sum so the 58 is not allowed, leaving 49 and 67 which is in agreement with the method we mentioned first here (not that we would expect it to be different as it is just two aspects of the same method - just dividing the sets in a different order).
So, looking at the 49 67 76 and 94 combinations, let's spot anything that doesn't fit (green) - note that there is no 8 in there so we can also spot that (red).
Giving this.
Now, we can put the 9 in top of the 16 in 2, spot it; put the 7 in the bottom (nothing to spot); put the 8 in the only space left in the 34 in 5; and finally, put the 9 in the right cell of the 22 in 3.
And, that is all there is to it.
Comparing it with the computer-generated solution shows that we got it right.
One other method (STEP 4 if you like) is that if you have two cells in the same sum and they both have only two possible values then, those two values cannot appear in any other cells in that sum.
In the example on the right, you can see that in cells A and E, the only two values that are available are 8 and 9. We don't know which goes where but we do know that they are the only two numbers that can go in those two cells and therefore they cannot go anywhere else. As a result, we can eliminate those numbers from any other unassiged cells so in cell C, we can spot out the 8 and in cell F, we can spot out the 9.
This also works with 3 cells with only the same 3 values - these being eliminated from the other unassigned cells (and 4, and 5 and so on).
You might notice that in cells C and F, the 5 and 6 are available and they are the only cells in that sum that use them - even though they have other numbers available (before we spotted the 8 and the 9 out of them). As a result of this, we could eliminate the numbers other than the 5 and 6 from cells C and F as they cannot be present - the 4 and 5 are the only numbers that can be. This is just an inverse logic version of the previous example. Similarly, this can also work with 3s and 4s so if you had 3 cells with, say, a 2, 5 and 9, then the other values in those three cells can be spotted out.
So, to solve a Kakuro, you start of with step 1, then, when that ceases to function, step 2, then back to step 1 again and so on, until you have gone through all of the methods you know or the puzzle is finished.
All of this might seem a bit long-winded. However, as you do more of these puzzles, you will get to know which intersecting combinations produce unique numbers (such as 3 in 2 intersecting with 4 in 2, producing a 1 and thus the 2 and 3 in the other cells) and so on. Eventually, you will be able to do them fairly quickly. Although these are based on a set of mathematical sums, you will find - at least while you are using the spot method - that logic will save you from doing the maths. Again, in your intersecting 3 and 4, the 1 will produce a 2 and 3 in the appropriate cells just using the spot patterns rather than the maths.
Good luck.
Copyright ©2019-2023 Paul Alan Grosse.